On Saturday, I gave the keynote talk at the Manhattan MATHCOUNTS contest. I haven’t had so much fun giving a math talk in a long while!
I was never exceptional at math contests, but I love them. I think they’re fun challenges and they create a vibrant community; used well they are a good tool in mathematics education. However, most contests also promote bad habits. They lead students to focus on speed and winning over deep thought. They encourage students to learn a few tricks well and memorize useless facts. They further perpetuate the myth that math is about speed, even though real-world problems take days, months, or years to solve. Hence, my talk was about transitioning to solving “big” problems. For my own reference later as well as for anyone who is interested, here’s a log of what I said and how I structured the talk.
Setting the Stage
I began by asking the room to raise their hands if they had ever spent more than one minute on a math problem, and all the hands went up. “More than five minutes?” “More than an hour?” Now many of the hands were down. “More than a day?” Few hands were still up. “More than a month? More than a year? More than five years?” (That last one was especially unlikely for 12-year-olds!)
The real problems in the world, I explained, take a long time. Proving a theorem, building a bridge, creating Facebook or Google — these take years! So I encouraged them to think about mathematics in a different way. Instead of contest thinking like“how fast can I solve these problems,” or “do I have the sides of a 30-60-90 right triangle memorized,” or “do I know the perfect squares up to 25 squared,” get practice thinking deeply about mathematics.
I told them about Maryam Mirzakhani. She’s one of the best mathematicians of our time, a winner the Fields Medal (the “Nobel Prize” of mathematics). It was important to me to show a woman doing mathematics at the highest levels, and I also wanted to go with someone currently living. I decided to go hard on establishing her credentials and to say “she” several times, but I was very careful not to say that she was the first woman to win the Fields Medal.
I debated that choice for a long time before the talk. Ultimately, I wanted a woman winning the Fields Medal to seem normal. There is a time when women in math must reckon with their underrepresentation, but MATHCOUNTS, which has a relatively large number of girls, is not that time. I was also wary of Einstein’s strange praise of Emmy Noether (one of the most brilliant mathematicians of the 20th century) in the obituary he wrote: “the most significant creative mathematical genius,” he wrote, “thus far produced since the higher education of women began.” The latter portion of the sentence was thoroughly unnecessary for Emmy Noether. Similarly, saying that Mirzakhani is the first female winner of the Fields Medal makes the gender dynamics front and center instead of her raw mathematical accomplishment. (Meanwhile, for the historical record, Einstein was a huge supporter of Noether and the reason she received a paid university position at all!)
Anyway, I’d brought up Mirzakhani because I wanted to share this quote from a Quanta article:
Mirzakhani likes to describe herself as slow. Unlike some mathematicians who solve problems with quicksilver brilliance, she gravitates toward deep problems that she can chew on for years. “Months or years later, you see very different aspects” of a problem, she said. There are problems she has been thinking about for more than a decade. “And still there’s not much I can do about them,” she said.
In short, if a scholar of this magnitude does not think speed is important, then why should you? Think deeply, not quickly.
With that, it was time to tell a story that reinforced this idea.
The Twin Primes Conjecture
There has been much recent progress on the Twin Primes Conjecture and it is a very approachable topic. It was to be my avenue in, the bit of mathematical culture through which I could convey that serious breakthroughs take a long time. I began by talking about how it was open since at least 1860; I wanted to show how mathematical results build upon one another, the partial results that come over years of work and progress from many mathematicians.
One of the early results on the twin primes conjecture is that the sum of the reciprocals of the twin primes converges, but I needed to introduce infinite summations for middle schoolers who might not have seen them. I talked about how the sum of the reciprocals of the powers of two converge, but the sum of the reciprocals of the positive integers do not; I also explained that it had been proven that the sum of the reciprocals of the primes diverges while the sum of the reciprocals of the twin primes converges.

This allowed me to point out that we proved something about the sum of the reciprocals of the twin primes without knowing how many there were or what they converged to, hinting at nonconstructive proof. An analogy helps explain the significance of this result: there are a lot fewer twin primes than primes; they are somehow “sparse” like the powers of 2 are sparse. I also pointed out that we might see the convergence result as a “bad” result, because we were hoping to prove that there are infinitely many twin primes, and the convergence leaves open the possibility they are finite. However, no result should be seen as bad, because everything gives insight.
From there, I outlined some of the results up through 2005 in the effort to prove the conjecture. The idea was to tell a story. Look at this steady advancement of mathematics. I was able to talk about how we build results upon other results, and to demonstrate that these real advances take time, returning to my theme that it is great to think slowly but deeply.
Then I jumped to the present day with Yiting Zhang’s result, and I got a nice laugh from saying that he made great progress by showing that there are infinitely many pairs of prime numbers… that are within 70,000,000 of each other! (Considering that we were aiming for infinitely many “2” apart, this still seems far off — but again, partial results are key!) From there I talked about the wonderful online collaboration between mathematicians to narrow 70,000,000 to 246.
Finally, to close off this topic I gave the students a challenge they could take home: to determine how many “prime triplets” there are, i.e. sets of three primes where each differs by 2 from the previous.
By the end of this, I felt like I’d communicated a strong component of mathematical culture and how progress is made. I felt like I’d done good work explaining to students that they must think deeply and take their time. In short, I felt like I had re-aligned them from the typical contest mindset.
Now, the challenge was to switch to doing mathematics. Even if they acknowledged the value of deep thinking and taking their time, they still were not empowered to do so. The problem was that with a 45-minute talk, half of which was already over, there simply wasn’t time for students to solve a “big” problem themselves. (In fact, I joked early on about how they shouldn’t fear, my talk would not be a year in length!)
Transitioning to a Problem
Something which I think gives many students difficulty approaching mathematics is the appearance of brilliance. Don’t get me wrong, I don’t doubt the existence of brilliance. However, it often seems as if proof methods and ideas “come out of nowhere” and someone simply must be a genius to discover them. I decided that if we couldn’t actually solve a problem somewhere, I could at least dispel this myth. Seemingly arbitrary but effective moves actually come from looking at patterns, experience, and building a chain of (often ineffective) ideas.
The problem was to take a wheel divided into 6 sectors. As many times as you want, you may add 1 to any two adjacent sectors, like this:
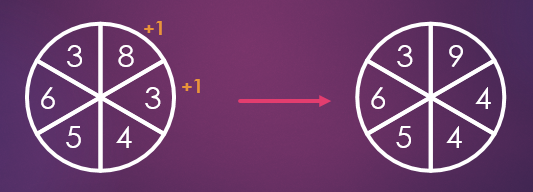
Is it possible, through these moves, to get from the starting wheel

to a final wheel where all the numbers are equal?
You’re welcome to try it out yourself before moving on!
I gave a warm-up problem (where it was easy to find moves leading to the goal wheel), and then we shifted to answering the problem. I told the students that if they were approaching this question, they would probably experiment for a while and get a feel for it. Then they’d look at all their attempts to see if there were any patterns in how this worked.
To save time for the talk, I gave the students a grid of 15 different states of the wheel that are achievable, perhaps the results of their experimentation. Then I gave them two minutes amongst themselves to look for patterns and see what they could discover. I wasn’t expecting them to solve the question: after all, this is intended to be a problem that they might spend hours upon! Instead, they should look for insights to push their thinking forward.
The students came up with some nice ideas. One student suggested that perhaps every attainable wheel has two equal numbers that appear. Although this was true in all of my examples, further experimentation showed that was not the case. We set for ourselves a goal of finding a wheel with all different numbers (which we did). Another student brought up the maximum difference between the highest and lowest values on the wheels (unbounded). Although these ideas did not work, they gave us nice results about what wheels were achievable, and I wanted the students to recognize that these results were valuable even when they did not solve the problem. It’s like proving that the sum of the reciprocals of the twin primes converges.
Then a student made a lovely observation: every wheel had exactly two odd numbers on it. Fascinating! Was that always true, I asked?
We soon discovered a wheel with zero odd numbers. However, it was rather interesting that we found 0 odd numbers, and we found 2 odd numbers. Can you have just one odd number? No, you can’t!
This leads you to realize that the sum of the numbers on all the wheels is even; this is easy to prove because each move adds 2 to the total. This partial result still does not prevent finding an attainable wheel with all six numbers equal, since such a wheel would also have an even sum. Again we did not solve the problem, but this is still strong progress! We now have a theorem that rules out many other wheels.
Perhaps we should take a step back. Using the sum of all the numbers is only using part of how the game works. It would still be true even if you were allowed to add two 1’s to any two sectors. We need to find an idea that takes advantage of the fact that the two 1’s must be next to each other. I challenged them to see if they could think of something.
One student did (although I think he had seen something like this before), and we soon narrowed down on creating an alternating sum of the numbers in the wheel, like this:

Now, adding two adjacent 1’s leaves the total unchanged! A wheel with all numbers equal has an alternating sum of 0, but our starting position has an alternating sum of 2! Hence, we know that we cannot attain all numbers equal.
Imagine, I told the students, that you had not solved this problem and someone came up to them with this proof by taking the alternating sum. They might look and say, “That person is brilliant! I would never have come up with that.” That ignores the way that all of this partial work and ideas built on each other; the “brilliant” person did not start out by taking the alternating sum! (Unless they’d seen similar problems before.) Playing around with it led us to counting odd numbers, which led to taking a sum; then seeking a way to think about adjacency led us to the alternating sum. Each step makes sense, in the context of thinking deeply about this problem.
It’s easy to imagine spending a long time on this problem. Perhaps one day, you come up with the idea of counting odd numbers, and you conjecture that there are always 2 odd numbers in an attainable wheel. However, then you discover a wheel with 0 odd numbers, and you conclude that your conjecture was false. You might decide it’s not worth looking at odd numbers. But perhaps you come back to it a day or two later, and, frustrated, you think about odd numbers again — then you realize that there are no wheels with exactly 1 odd number entry, and you’re making progress again! It takes time and persistence, and that is what I want the students to learn.
Concluding Thoughts
I ended by saying how no mathematical proof literally comes out of nowhere. It comes from someone who thought deeply about the problem and found a way through it. I talked about the idea of “following your nose”, and looking for maneuvers that seem appealing even if you are not sure they will work. I also pointed out that the next time a similar problem comes up, one where odd/even plays a role or where an alternating sum is useful, this is now a tool in their toolbox.
In short, it is important to develop strong habits of mind, stamina, and a willingness to try many things. That was my concluding message to the students in their next steps to solving big problems.
I wish my college math majors could have heard your talk. Are you available for speaking engagements? (-:O
Also, when did Mathcounts start having keynote talks? I don’t remember them from when I was a middle schooler. Although I suppose I might have skipped them or tuned them out. Or maybe Manhattan is just cooler than Los Angeles.
Yeah, Manhattan is just cooler – none of the other boroughs here do it. But MATHCOUNTS Manhattan is *huge*, and amazingly well organized. They need time to grade and rank everyone, so the speaker like me is basically a delaying tactic!
(I do, by the way, intend to use this talk in other settings!)
Next time you come to visit San Diego, maybe I can drag you over to USD. (-:
Lovely article! The one sour note was the suggestion out of nowhere that the student who came up with the crucial idea had seen something similar before. Maybe you had some concrete reason for thinking so – but if not, why not allow the student to have had a good idea?
Oh, I did! I wonder if he’d seen the idea before, but in the talk I just took the idea and ran with it.
Also, thanks!
Sorry, I wasn’t clear. I meant that here, in the article, you “stole his thunder” by suggesting to us (the readers) that he had seen it before. Of course, you may be right, but I too often see adults assuming that children who have a good idea must have got it from somewhere, rather than having thought of it, and I’ve become sensitised to it because I think it’s sad – in my experience, children often have good ideas for themselves! I’m sure you didn’t mean to put him down.
Ah! Yes, I think that’s completely fair. I think part of my guess is because I expected a couple of students in the audience to have seen something like this already and to be a few steps ahead of me. But you’re right! I should have let it stand.
The lesson that hard problems are all about effort and persistence is really key for many bright kids, (even beyond the mathematically sophisticated mathcounts crowd). The wheel problem and many others like it are routinely thought about and explored in math circles in some countries and can easily be introduced to elementary and middle school kids everywhere in the world. Kids love exploring these type of problems and playing with them until they find something interesting and over time they can learn a tremendous amount of problem solving, creative thinking, and most importantly a comfort dealing with problems that don’t have instant answers. Until our school establishment realizes that this is something bright kids everywhere badly need exposure to, real mathematics education will remain stuck in the fringe for the lucky few who know about these opportunities, while the rest are forced to mimic endless procedures without any understanding of what math is.